Spurious correlations?

Time and again, the rather simple-minded saying falsely attributed to Winston Churchill pops up: “The only statistics you can trust are the ones you have falsified yourself.” By the way, probably Josef Goebbels is the originator (according to Werner Barke in: ‘I only believe statistics…. What Winston Churchill is supposed to have said about numbers and statistics – and what he really said’). But this only in passing.

First of all, statistics is nothing other than collecting data, presenting them in the form of tables and graphs, analysing them and, if necessary, interpreting them. It is useless to enumerate all the places we meet statistics, because there is no area in which statistics does not play a role.

But why do people accuse others of falsifying when collecting or compiling data? According to my observation, this alleged ‘wisdom’ is always used when people are confronted with statistics whose possible interpretation does not suit them, which in my opinion says more about the quoting person than about the statistics.

I think there are several reasons for this, which are not only related to human capital. One major reason seems to me to be that many people obviously don’t have a clue about statistics and let us know this – even if unconsciously – in a way that attracts public attention. Talk shows, interviews, press conferences, parliamentary debates, newspaper articles and even history books are full of it. This points, on the one hand, to the confusion and mixing of causality and correlation and, on the other hand, to the fallacious assumption that one has to falsify statistics in order to suggest a desired interpretation.

Let us first consider the first reason. Correlation means that there is a mathematically describable relationship between two or more characteristics, events, states, etc., but this does not mean that one determines the other. Causality means that one thing does cause another. Thus, as a sixth-former, I was taught in the course of the examination of National Socialism that large numbers of the unemployed voted for the NSDAP, which is complete baloney and was based only on the fact that the authors simply overlooked the fact that high NSDAP election results at times of high unemployment do not mean that the unemployed were classic NSDAP voters. This as an example of what the consequence of such confusion can be.

A graphic example

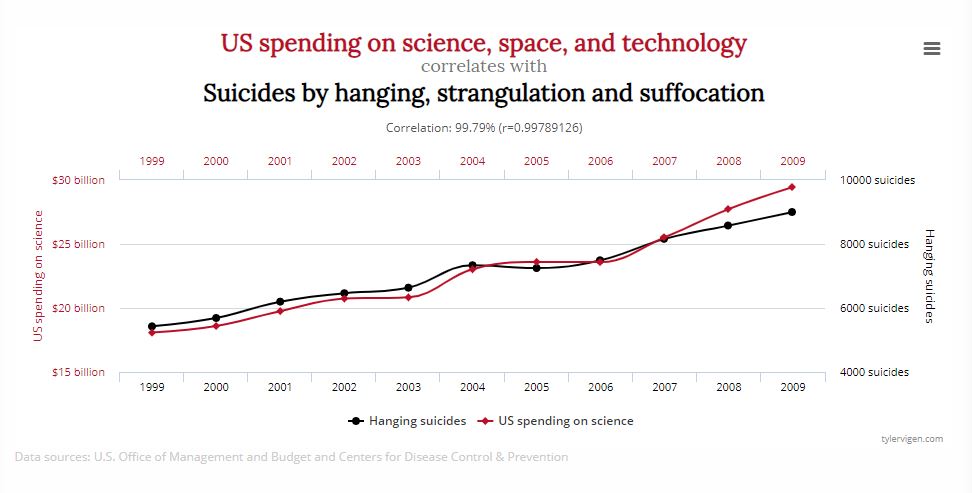
I would trust the orange-skinned ex-president to reduce government spending on science based on this graphic. Other absurd and funny examples can be found quite easily (search for spurious correlation on the Internet).

A much more recent example comes from the ‘Non-statistics of the Month’ (https://www.rwi-essen.de/unstatistik/), published in December 2021. Dr. Ute Bergner, physicist and independent member of the Thuringian state parliament handed over to the Minister of Health a white paper that showed a positive correlation (0.31) for the period between the 36th and 40th calendar week between excess mortality in the federal states and their vaccination rate. For better understanding: A correlation of 0.31 is ridiculously low and not significant, i.e. it can also be a coincidence. The maximum negative correlation is -1 and the maximum positive correlation is +1). And why just the weeks 36-40? Quite simple: Because the correlation for the period from week 20 -40 showed an even worse value (0.14) and for weeks 36-44 even a negative and higher correlation (-0.37).

According to the EMIS (Emerging Markets) report of 2017, a statistically relevant correlation exists in Switzerland between the assessment of the personal income situation and sexual satisfaction, which brings us to point two, the interpretation. Harlequin fans are requested to reflect briefly on the assumption that just popped into their heads. ‘Wealthy people have better sex’, or ‘Poor, but more fun in bed’?

Those who actually want to use statistics for opinion manipulation are typically not so naive to believe that falsification helps, when it can be done much more subtly. Omitting or emphasizing is much better, because it is not a lie, as Dr. Bergner’s example shows. If we assume for the moment that the lady had to take at least basic courses in statistics in the course of her studies, i.e. that she knew about the dubiousness, she represents a wonderful example of combining both possibilities: Making correlation look like causality AND omitting/emphasizing. If, however, our assumption she acted deliberately is wrong, it seems to me to be appropriate to breathe a sigh of relief that the lady went into politics and not into reactor technology.

Original text: RGE
English translation: BCO